Kademlia 算法抄写
本文基本参考了Wiki 上的 Kademlia。同时参考了文献 Kademlia: A of Peer to peer information system Based on the XOR Metric (其本质上只能说是一种抄写)
最早先的 P2P 网络,比如 Napster 是通过一个中心化的 Hash Table 来进行查找。后来的 P2P 网络,比如 Gnutella,使用 Flooding 算法查找所有在线的节点。现在的 P2P 网络则大多是使用分布式的 Hash Table 来实现查找。分布式 Hash Table 存储了资源在网络上的位置。
节点的距离
节点的距离通过节点 ID 之间的异或操作(XOR)得到。显然节点间的距离有如下特性:
- 两个节点间的距离是随机的
- 节点与自身的距离是0
- 对称性。A 到 B 的距离和 B 到 A 的距离相等
- 三角不等。distance(A,B)+distance(B,C) <= distance(A,C)
还有一个重要的特性,距离不仅可以应用在节点之间,也可以应用在节点和键值之间。这在键值查找中很有用。
路由表
假设每个节点的 ID 是 N bits,那么每个节点需要维护 N 个列表(又称之为 K 桶)用于存储。列表里面的元素则存储了其他节点的信息(比如 IP 端口啥的)。每个列表存储的节点特性如下:
每个列表对应于与节点相距特定范围距离的一些节点,节点的第 n 个列表中所找到的节点的第 n 位与该节点的第n位肯定不同,而前 n-1 位相同。
举个栗子。如下图所示,节点使用 3 个 bits 的 ID。在下面的网络里面总共有 7 个节点。对于第 6 个节点(标号为 110 )而言,根据 K 桶的定义,该节点应该有 3 个 K 桶。
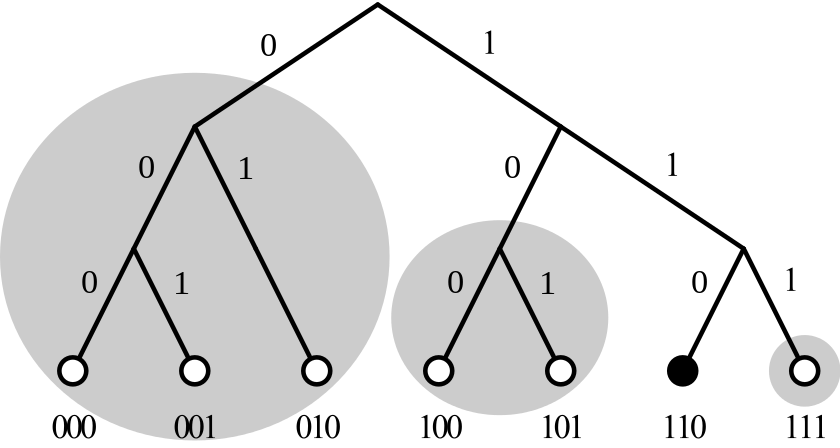
那么:
- 第一个 K 桶,其可能的节点为左边灰色框内的三个(标号 000/001/010)。因为它们的第一位与 110 不同。
- 第二个 K 桶,其可能的节点为中间灰色框内的两个(标号100/101)。因为它们的第二位与 110 不同,而第一位与 110 相同。
- 第三个 K 桶,其可能的节点为右边灰色框内的一个(标号111)。因为它的第三位与 110 不同,而第一第二位与 110 相同。
推而广之,第一个列表理论上可以填充一半的全部节点,而第二个列表可以填充1/4的全部节点,依次类推。当然列表里面的容量不可能是无限制的,可以取一个约定的值 K 作为每个列表的最大容量。列表在 Kademlia 网络里面又称为 K 桶。显然大部分的数据都会集中在前面几个列表中,而后面的列表很可能是空的(网络中的可用节点数据远小于 ID 的可能数目)。当某个列表满,且发现了新的符合要求的节点时:
首先检查K桶中最早访问的节点,假如该节点仍然存活,那么新节点就被安排到一个附属列表中(作为一个替代缓存).只有当K桶中的某个节点停止响应的时候,替代 cache 才被使用。换句话说,新发现的节点只有在老的节点消失后才被使用。
协议消息
消息分为四种:
- PING 检查节点是否在线
- STORE 在某个节点中存储一个键值对
- FIND_NODE 返回对方节点桶中离请求键值最近的 K 个节点
- FIND_VALUE 与 FIND_NODE 一样,不过当请求的接收者存有请求者所请求的键的时候,它将返回相应键的值
定位节点
节点的查询可以异步进行,也可以同步进行,不过同时查询的数量有限制(一般是3)。假设节点 A 要查询某个键值,则在查询时,先在自己的 K 桶中找到离所查询键值最近的 K 个节点。然后对这些个节点发起 FIND_NODE 操作,如果它们知道离被查键更近的节点,就返回它们(最多 K 个)。节点 A 始终维护一个 K 长度的节点列表,来存储当前知道的最近节点。如此不断地迭代操作,就能够搜索到离键值越来越近的节点。当某一次迭代的结果没有比前次节点更近,则迭代终止,此时的结果即是全网络中离查询键值最近的节点。
这么说来,感觉之前有国人做的 Vagga 是不是就是滥用了同时查询限制,疯狂进行 FIND_NODE 导致怨声载道。。。
定位资源
定位资源时,如果一个节点存有相应的资源的值的时候,它就返回该资源,搜索便结束了,除了该点以外,定位资源与定位离键最近的节点的过程相似。
考虑到节点未必都在线的情况,资源的值被存在多个节点上(节点中的 K 个),并且,为了提供冗余,还有可能在更多的节点上储存值。储存值的节点将定期搜索网络中与储存值所对应的键接近的 K 个节点并且把值复制到这些节点上,这些节点可作为那些下线的节点的补充。另外,对于那些普遍流行的内容,可能有更多的请求需求,通过让那些访问值的节点把值存储在附件的一些节点上(不在 K 个最近节点的范围之类)来减少存储值的那些节点的负载,这种新的存储技术就是缓存技术。通过这种技术,依赖于请求的数量,资源的值被存储在离键越来越远的那些节点上,这使得那些流行的搜索可以更快地找到资源的储存者。由于返回值的节点的 NODE_ID 远离值所对应的关键字,网络中的“热点”区域存在的可能性也降低了。依据与键的距离,缓存的那些节点在一段时间以后将会删除所存储的缓存值。DHT 的某些实现(如 Kad )即不提供冗余(复制)节点也不提供缓存,这主要是为了能够快速减少系统中的陈旧信息。在这种网络中,提供文件的那些节点将会周期性地更新网络上的信息(通过 NODE_LOOKUP 消息和 STORE 消息)。当存有某个文件的所有节点都下线了,关于该文件的相关的值(源和关键字)的更新也就停止了,该文件的相关信息也就从网络上完全消失了。
加入网络
对于一个想要加入网络的新节点 A,需要知道一个已经在网络里面的某个节点 B,由这个节点来引导新加入的节点进行初始化。
首先 A 节点需要生成一个随机且未被人使用的 ID 号,直到离开网络,该节点会一直使用该 ID 号。然后 A 节点需要将引导节点 B 加入自己的 K 桶中,然后向节点 B 发起 NODE_LOOK_UP 来定位自己( NODE_LOOK_UP 在文献里指的是找到离某个节点最近的 K 个节点)。这样其他的节点就会将 A 节点加入自己的 K 桶中。同时也能够使用那些查询过程的中间节点(位于新加入节点和引导节点的查询路径上的其他节点)来填充新加入节点的K桶。
最初,节点只有一个 K 桶(覆盖所有的 ID 范围)。当有新节点需要插入该 K 桶时,如果 K 桶已满,K 桶就开始分裂。其实我认为这里 Wiki 上的已满有歧义,这里的满应该不是指 K 桶内的元素达到了 K 个,而是要插入的节点已经不符合该 K 桶的覆盖范围,即覆盖范围包含了其自身 ID 的时候。实际的情况如下图所示。
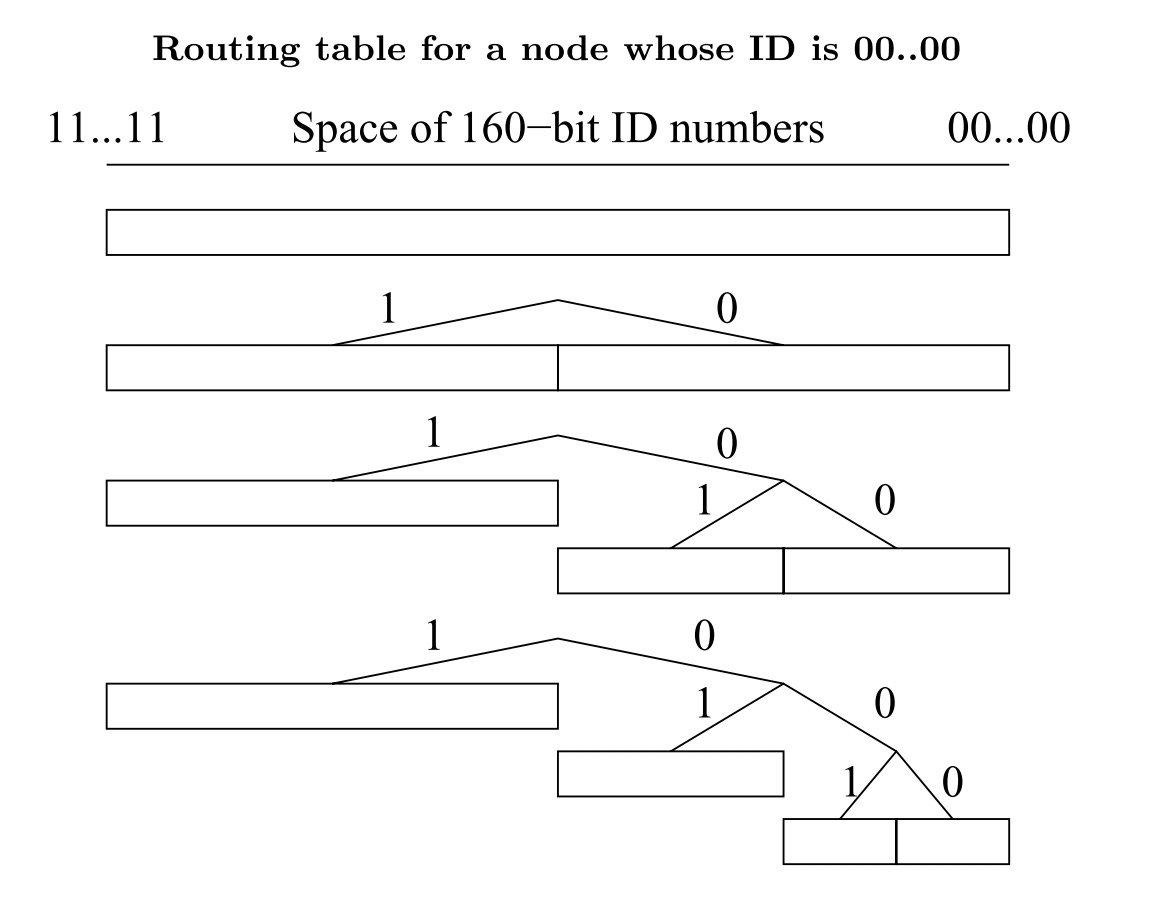
实际上还有一种优化的骚操作,但我愣是没看懂。所以只能摘抄在下面
对于节点内距离节点最近的那个K桶,Kademlia可以放松限制(即可以到达K时不发生分裂),因为桶内的所有节点离该节点距离最近,这些节点个数很可能超过K个,而且节点希望知道所有的这些最近的节点。因此,在路由树中,该节点附近很可能出现高度不平衡的二叉子树。假如K是20,新加入网络的节点ID为“xxx000011001”,则前缀为“xxx0011……”的节点可能有21个,甚至更多,新的节点可能包含多个含有21个以上节点的K桶。(位于节点附近的k桶)。这点保证使得该节点能够感知网络中附近区域的所有节点。
在文献中的说明如下
One complication arises in highly unbalanced trees.Suppose node u joins the system and is the only node whose ID begins 000.Suppose further that the system already has more than k nodes with prefix 001.Every node with prefix 001 would have an empty k-bucket into which u should be inserted, yet u’s bucket refresh would only notify k of the nodes.To avoid this problem, Kademlia nodes keep all valid contacts in a subtree of size at least k nodes, even if this requires splitting buckets in which the node’s own ID does not reside.Figure 5 illustrates these additional splits.When u refreshes the split buckets, all nodes with prefix 001 will learn about it.
查询加速
因为 Kademlia 使用异或距离来进行路由查找。对于一个 n bits 定义的网络,在一个节点上执行查找操作的时间复杂度为 \(log(n)\) 。这个可以使用位组(多个位联合)来优化。位组也可以称之为前缀。对一个 m 位的前缀来说,可对应 \(2^m-1\) 个K桶。(m位的前缀本来可以对应 \(2^m\) 个K桶)另外的那个 K 桶可以进一步扩展为包含该节点本身 ID 的路由树。这个特殊的 K 桶应该和之前没懂的优化骚操作有关。一个 b 位的前缀可以把查询的最大次数从 \(log(n)\) 减少到$ log(n/b) $. 这只是查询次数的最大值,因为自己 K 桶可能比前缀有更多的位与目标键相同。
感想
分布式真有意思,可惜自己的智商是个阻碍。。。