信号处理笔记（一）

年后要去做算法相关了，赶紧把信号处理的知识补一补。基本算是胡广书《数字信号处理》的笔记。

LSI 系统

LSI 系统即线性时不变系统，同时具有线性和移不变性。

• 线性：\(LSI[A(n)] + LSI[B(n)] = LSI[A(n)+B(n)]\)
• 移不变：\(LSI[A(n)]=y(n) \rightarrow LSI[A(n-m)]=y(n-m)\)

线性卷积

卷积是一个蛮重要的概念了，我们假设一个 LSI 系统的冲激响应是 \(h(n)\)，那么该系统对信号 \(x(n)\) 的响应为

\[y(n)= \sum_{k=- \infty}^{\infty}x(k)h(n-k)\]

简记为 \(y(n)=x(n)*h(n)\)。对于因果系统而言（即 \(n \lt 0\) 时 \(h(n)\equiv 0\)），意味着

\[y(n) =\sum_{k=0}^{\infty}h(k)x(n-k)\]

LSI 系统的频率响应

对于一个 LSI 系统（线性时不变系统），它的冲击响应为 \(h(n)\)。如果输入信号为 \(x(n) = e^{j \omega n}\) 。其中 \(\omega\) 为圆频率，单位 rad。

那么根据欧拉公式有

\[ e^{j \omega n} = cos(\omega n)+j\ sin(\omega n)\]

由 \(x(n)\) 引起的输出为

\[\begin{split}y(n) &= \sum_{k=-\infty}^{\infty }h(k)x(n-k) \\\ &= e^{j \omega n} \sum_{k= - \infty}^{\infty}h(k)e^{-j \omega k} \\ &=e^{j \omega n}H(e^{j \omega})\end{split}\]

意味着输出 \(y(n)\) 也包含了同频率的复正弦信号，但受到信号 \(H(e^{j \omega})\) 的调制。因此称 \(e^{j \omega n}\) 为系统的特征函数。\(H(e^{j \omega})\) 为系统的频率响应，又称为系统的特征值。其实上式是 \(h(n)\) 的离散傅立叶变换。这个 \(H(e^{j \omega})\) 又可以进一步地分解为实部和虚部，或者幅度和相位。公式如下

\[H(e^{j \omega})=H_R(e^{j \omega})+jH_I(e^{j \omega})\] \[H(e^{j \omega})=|H(e^{j \omega})|e^{j \phi(\omega)}\]

如果我们将式中的 \(e^{j \omega}\) 替换为 \(z\) ，那么我们就得到了 z 变换的公式，\(H(z)\) 是系统的转移函数

\[H(z)=\sum_{n=- \infty}^{\infty}h(n)z^{-n}\]

有一点融汇贯通的地方在于，设计一个数字滤波器（或者系统）就是设计一个转移函数 \(H(z)\)。

确定性信号的相关函数

相关系数

设 \(x(n)\) 和 \(y(n)\) 是两个能量有限的因果信号。相关系数定义如下

\[\rho_{xy} = \frac{\sum_{n=0}^{\infty}x(n)y(n)}{\sqrt{\sum_{n=0}^{\infty}x^2(n)\sum_{n=0}^{\infty} y^2(n)}}\]

上式中的分母其实是各自能量乘积的开方。且根据许瓦兹不等式有\(\lvert \rho_{xy} \rvert \leq 1\)。但 \(\rho_{xy}\) 仅反应了两个固定信号的相似程度，对于有一些相位差异的信号效果比较糟糕。因此需要引入相关函数

相关函数

定义

\[r_{xy}(m)=\sum_{n= -\infty}^{\infty}x(n)y(n+m)\]

为信号的互相关函数。其实相当于 \(x(n)\) 不动而 \(y(n)\) 左移 \(m\) 个单位相乘再相加。上式也可以改写如下

\[r_{xy}=\sum_{n=-\infty}^{\infty}x(n-m)y(n)\]

当\(y(n)=x(n)\)时衍生出自相关函数定义

\[r_{x}(m)=\sum_{n=-\infty}^{\infty}x(n)x(n+m)\]

但要注意的是，如果信号 \(x(n)\) 不是能量（有限）信号，那么其自相关函数可能为无穷。因此对于功率信号而言，需要将其相关函数定义如下

\[r_{xy}(m)=\lim_{N \rightarrow \infty} \frac{1}{2N+1}\sum_{n=-N}^{N}x(n)y(n+m)\]

\[r_{x}(m)=\lim_{N \rightarrow \infty} \frac{1}{2N+1}\sum_{n=-N}^{N}x(n)x(n+m)\]

这里通过定义还可以得到一个小小的推论，如果 \(x(n)\) 是周期信号，那么其自相关函数也是周期的，且与原周期一致。意味着无限的求和可以通过一个周期内的求和平均得到，即（下式中\(N\)为周期）

\[r_x(m) = \frac{1}{N} \sum_{n=1}^{N-1}x(n)x(n+m)\]

对于复值信号，相关函数应该改写如下

\[r_{xy}=\sum_{n=-\infty}^{\infty}x^*(n)y(n+m)\]

\[r_{x}(m)=\sum_{n=-\infty}^{\infty}x^*(n)x(n+m)\]

相关函数和线性卷积的关系

我们假设 \(g(n)\) 是 \(x(n)\) 和 \(y(n)\) 的线性卷积，即有\(g(n)=\sum_{m=-\infty}^{\infty}x(n-m)y(m)\)，对调 \(m\) 和 \(n\) 则有

\[g(m)=\sum_{m=-\infty}^{\infty}x(m-n)y(n)\]

而 \(x(n)\) 和 \(y(n)\) 的互相关函数为

\[\begin{split}r_{xy}(m)&=\sum_{n=-\infty}^{\infty}x(n-m)y(n) \\\ &=\sum_{n=-\infty}^{\infty}x[-(m-n)]y(n) \\\ &=x(-m)*y(m)\end{split}\]

同理对自相关函数有

\[r_x(m)=x(-m)*x(m)\]

但要注意，尽管相关和卷积的计算形式很相似，但是二者的物理意义是不一样的。相关反应的是两个信号之间的相关性，而卷积反应的是 LSI 系统输入输出以及单位抽样响应间的基本关系。

相关的实际应用

在实际的应用中需要注意两点。首先 \(x(n)\) 一般是有限长度的，那么自相关函数则应该改写为

\[r_x(m)=\frac1{N}\sum_{n=0}^{N-1-m}x_N(n)x_N(n+m)\]

其中 \(m \in [-(N+1), N-1]\)。上式仅计算了 \(0\) 到 \(N-1\) 部分。且要注意到 \(m\) 越大，其使用的信号有效长度越短，相关函数的性能就越差。一般要求 \(m \ll N\) 。且不管 \(x(n)\) 是功率信号还是能量信号，都需要除以数据长度 \(N\)

相关函数应用举例

用自相关函数可以检测信号中的隐含周期。例如信号 \(x(n)\) 由理想信号 \(s(n)\) 和 白噪声 \(u(n)\) 组成。假定 \(s(n)\) 的周期为 \(M\)，\(x(n)\) 的长度为 \(N\) 且 \(N \ll M\)，\(x(n)\) 的自相关函数为

\[\begin{split}r_x(m) &= \frac1N\sum_{n=0}^{N-1}[s(n)+u(n)][s(n+m)+u(n+m)] \\\ &=r_s(m) + r_u(m)+r_{su}(m)+r_{us}(m) \end{split}\]

正常情况下，我们可以认为 \(r_u(m)+r_{su}(m)+r_{us}(m)\) 都是比较小的（噪声嘛）。因此对 \(x(n)\) 贡献最大的项应该是 \(r_s(m)\)。又因为自相关函数的周期和原函数是一致的，且会在 \(m=0,M,2M,...\) 处出现峰值。

例1

设信号 \(x(n)\) 由正弦信号和白噪声叠加得到。正弦信号幅度为1，周期为 \(T=10\)，噪声方差为1，二者的长度均为 \(N=1000\)。那么信噪比为

\[\begin{split}SNR &= 10 \cdot \log_{10}[\frac{\frac1N\sum s^2(n)}{\frac1N\sum u^2(n)}] \\\ &=10 \cdot \log_{10}[\frac{\sum_{n=0}^{N}\sin^2{\frac {2\pi n}T}}{\sum_{n=0}^{N}u^2(n)}] \\\ &=10 \cdot \log_{10}[\frac{\frac NT \sum_{n=0}^{T}\sin^2(\frac {2\pi n}T )}{N}] \\\ &=10 \cdot \log_{10}[\frac{\frac NT \cdot \frac T2}N] \\\ &\approx-3.01\end{split}\]

如下图我们直接看 \(x(n)\) 的图像其实比较难看出它的正弦信号成分。

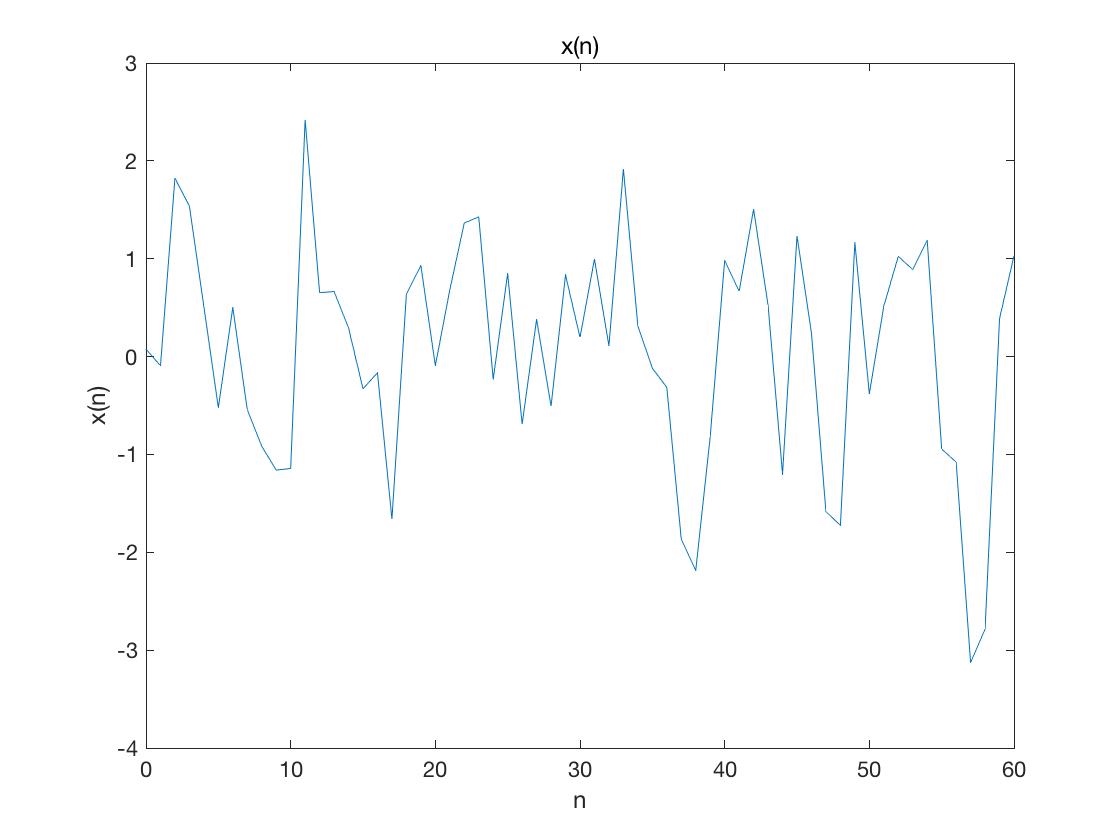
但如果我们观察它的自相关函数便可以很明显地看出其包含了正弦信号。

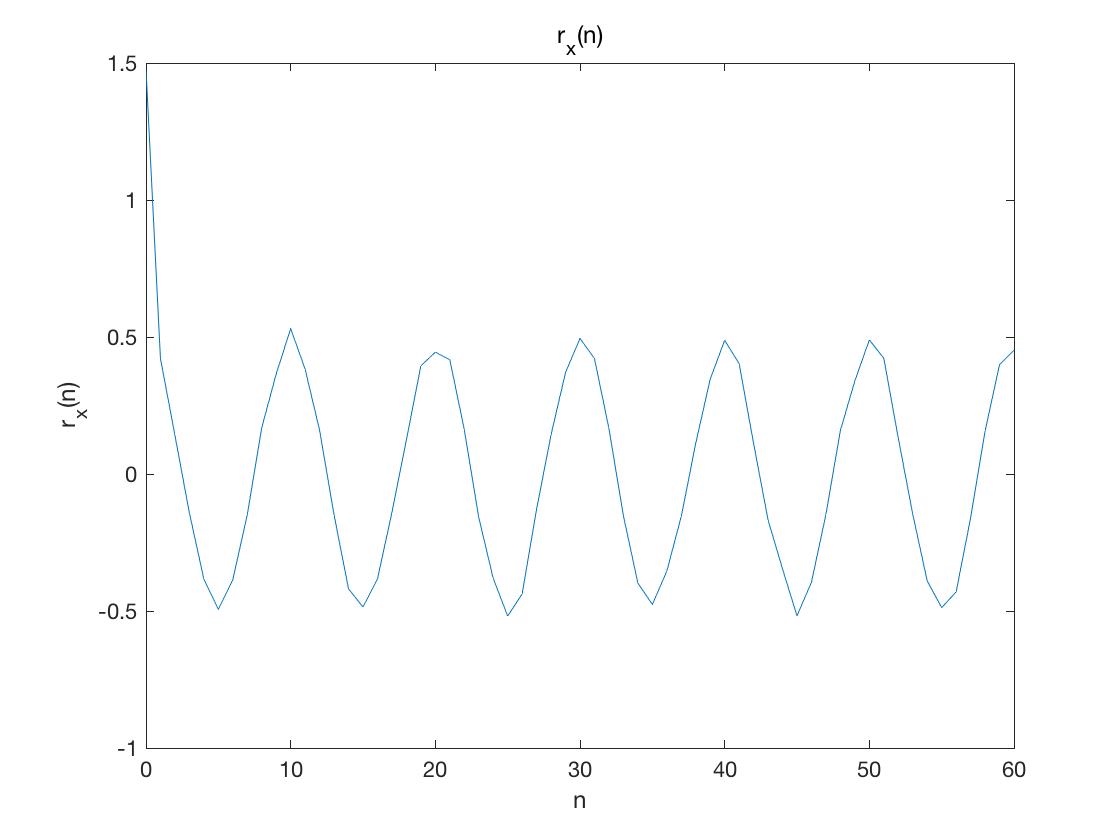
多说无益，我们上 matlab 代码。

clc
clear all
close all
N = 1000;
T = 10;
n = 0:(2*pi/T):(1000/(2*pi/T));
sn = sin(n);
un = randn(1, length(n));
xn = sn + un;

% 绘制原信号
figure(1);
plot(0:1:60, xn(1:61));
xlabel('n');
ylabel('x(n)');
title('x(n)');

% 计算自相关函数
rx=xcorr(xn,'biased');
rx=rx(length(xn):1:end);
figure(2);
plot(0:1:60, rx(1:61));
xlabel('n');
ylabel('r_x(n)');
title('r_x(n)');

例2

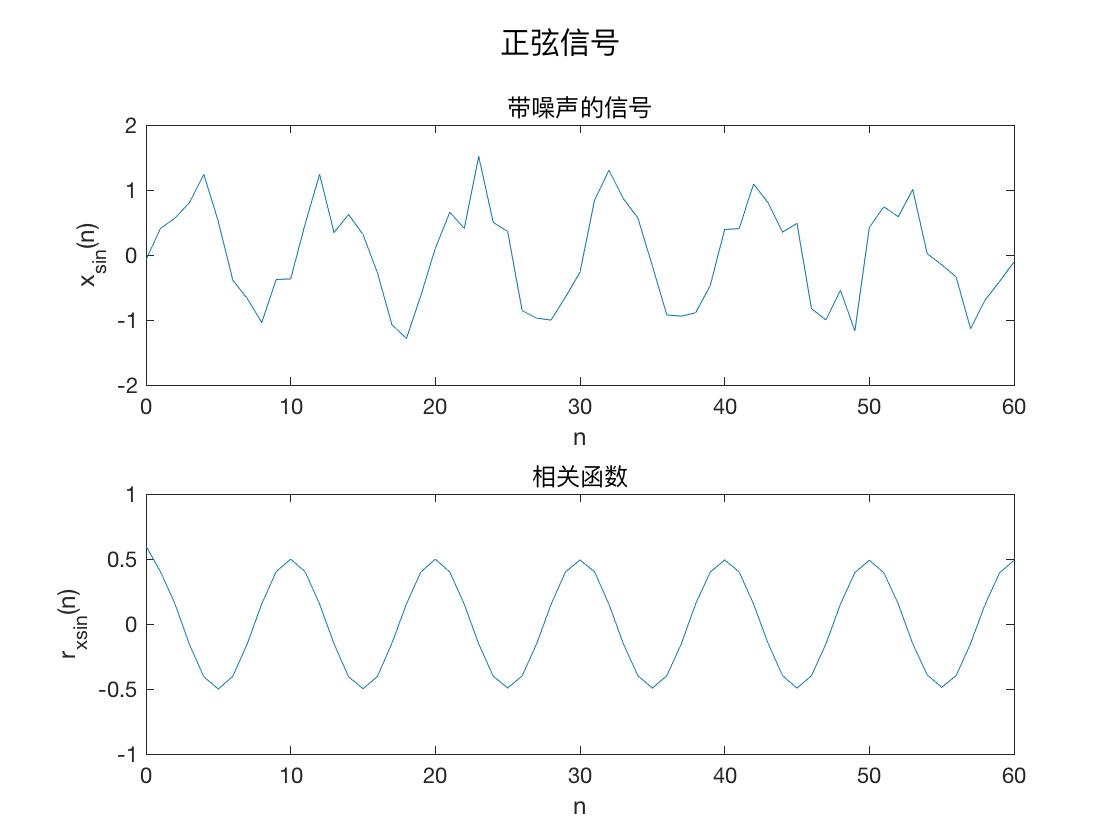
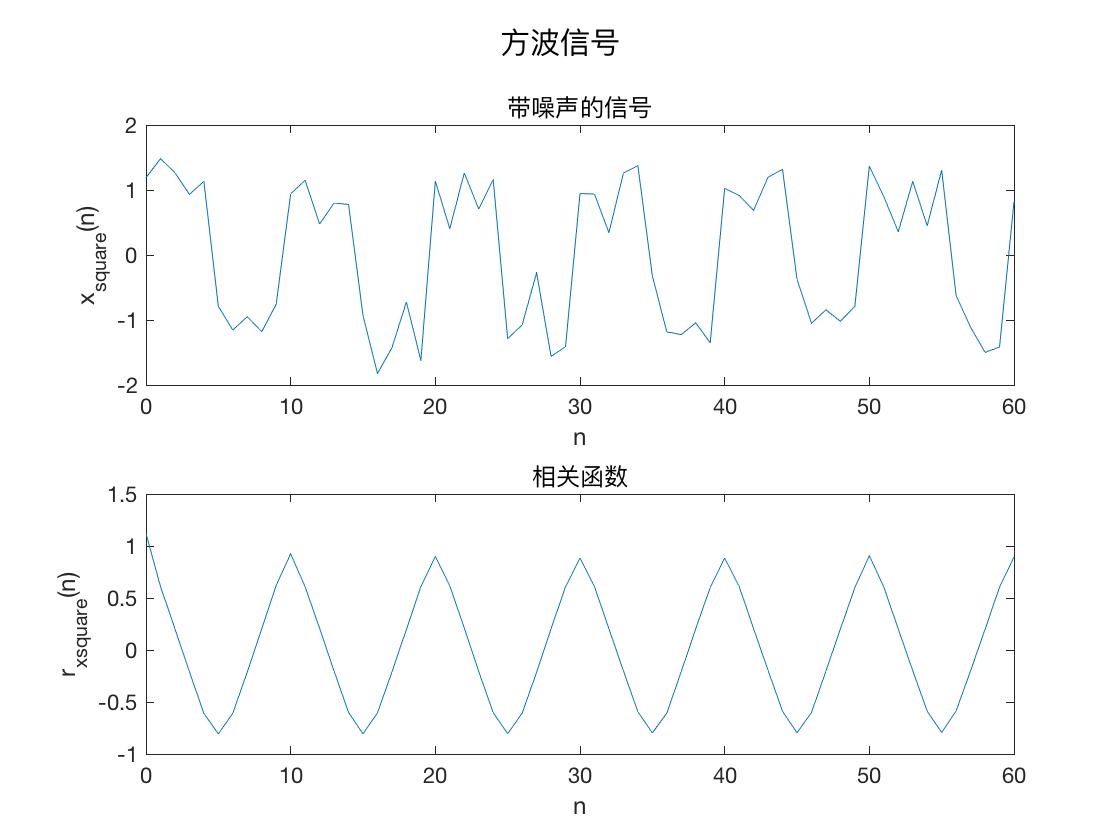
如果我们的白噪声方差为 0.1，那么假设我们有两个信号， \(s_{sin}(n)\) 还是上面的正弦量，而 \(s_{square}(n)\) 则是同周期的方波，定义如下

\[s_{square}(n)=\begin{cases} & 1& n \in [kT, kT+\frac 12 T),k=0,1,2...\\\ &-1& n \in [kT+\frac 12 T, kT + T),k=1,2,3... \end{cases}\]

同样我们有带噪声的两个信号 \(x_{sin}(n)=s_{sin}(n)+u_{sin}(n)\) 和 \(x_{square}(n)=s_{square}(n)+u_{square}(n)\)

那么其实我们可以从自相关函数上去区分这两个信号。

直接上 matlab 代码

clc
clear all
close all
N = 1000;
T = 10;
n = 0:(2*pi/T):(1000/(2*pi/T));
s_sin = sin(n);
u_sin = randn(1, length(n))/sqrt(10);
x_sin = s_sin + u_sin;
s_square = square(n);
u_square = randn(1, length(n))/sqrt(10);
x_square = s_square + u_square;

% 正弦信号
r_sin=xcorr(x_sin,'biased');
r_sin=r_sin(length(x_sin):1:end);
figure(1);
subplot(2,1,1); 
plot(0:1:60, x_sin(1:61));
title('带噪声的信号');
xlabel('n');
ylabel('x_{sin}(n)');
subplot(2,1,2);
plot(0:1:60, r_sin(1:61));
xlabel('n');
ylabel('r_{xsin}(n)');
title('相关函数');
suptitle('正弦信号');

% 方波信号
r_square=xcorr(x_square,'biased');
r_square=r_square(length(x_square):1:end);
figure(2);
subplot(2,1,1); 
plot(0:1:60, x_square(1:61));
title('带噪声的信号');
xlabel('n');
ylabel('x_{square}(n)');
subplot(2,1,2);
plot(0:1:60, r_square(1:61));
xlabel('n');
ylabel('r_{xsquare}(n)');
title('相关函数');
suptitle('方波信号');

根据下面的图像我们可以比较容易地分辨出正弦和方波。