信号处理笔记（二）

第二部分主要是 z 变换相关内容。

z 变换定义

对一个离散信号 \(x(n), n \in (-\infty, \infty)\)，z 变换的定义如下

\[X(z) = \sum_{n=-\infty}^{\infty}x(n)z^{-n}\]

其中 \(z\) 为一复变量。因为 \(n \in (-\infty, \infty)\)，上式也称之为双边 z 变换。那么如果 \(n \in [0, \infty)\) ，就变成了单边 z 变换

\[X(z) = \sum_{n=0}^{\infty}x(n)z^{-n}\]

同样的，如果我们已知 \(X(z)\) 及其收敛域 ROC 反求序列 \(x(n)\) 则称之为逆 z 变换。

z 变换与拉普拉斯变换

令 \(x_s(nT_s)\) 是由连续信号 \(x(t)\) 经抽样得到，即有

\[x_s(nT_s) = x(t)\sum_{n=-\infty}^{\infty}\delta(t-nT_s)=\sum_nx(nT_s)\delta(t-nT_s)\]

对上式取拉普拉斯变换，有

\[\begin{split}X(s) &= \int_{-\infty}^{\infty}x_s(nT_s)e^{-st}dt \\\ &=\int_{-\infty}^{\infty}[\sum_nx(nT_s)\delta(t-nT_s)]e^{-st}dt \\\ &=\sum_nx(nT_s)\int_{-\infty}^{\infty}\delta(t-nT_s)e^{-st}dt \\\ &=\sum_{n=-\infty}^{\infty}x(nT_s)e^{-snT_s} \\\ &=\int_{-\infty}^{\infty}x(nT_s)e^{-(snT_S)t}dt = X(e^{sT_s}) \end{split}\]

记 \(z=e^{sT_s}\)，将 \(T_s\) 归一化为 1，我们就能得到 z 变换的定义

\[X(z) = \sum_{n=-\infty}^{\infty}x(n)z^{-n}\]

记拉普拉斯变量 \(s=\sigma + j\Omega\)，且 \(\Omega=2 \pi f\)。\(\Omega\) 可以认为是相对连续系统及连续信号的角频率，单位 rad/s，则有

\[z=e^{sT_s}=e^{(\sigma+j \Omega)T_s}=e^{\sigma T_s}e^{j \Omega T_s}\]

再记 \(r=e^{\sigma T_s},\omega=\Omega T_s\)，则有

\[z=re^{j \omega}\]

\[X(z)=\sum_{n=-\infty}^{\infty}[x(n)r^{-n}]e^{-j\omega n}\]

注意到这个式子和傅立叶变换的相似之处。z 变换可以看成是信号乘以一加权序列 \(r^{-n}\) 后的傅立叶变换 \(X(z) = F[x(n)r^{-n}]\)。显然，当 \(r=1\) 时 z 变换就变成了离散序列的傅立叶变换。

z 平面和 s 平面

直接抄一张书上的图（Mac下数学绘图太麻烦了）

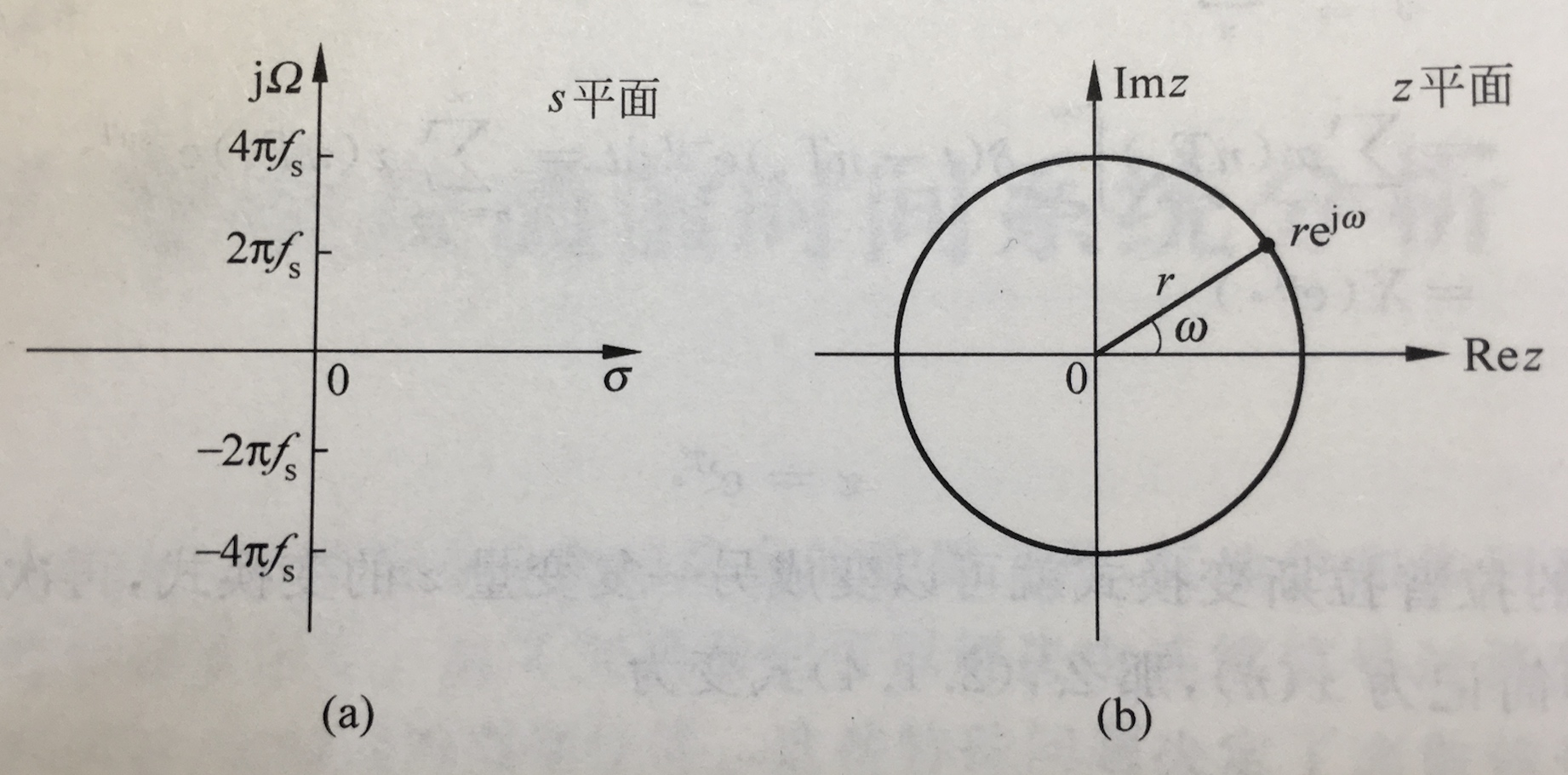
不难得到二者之间的对应关系

• 当 \(\sigma = 0\) 时， \(r=1\)。对应 \(s\) 平面的 \(j \Omega\) 轴。而 \(|z|=1\) 对应 \(z\) 平面半径 \(r=1\) 的圆。即当 \(z\) 仅在 \(j\Omega\) 轴上取值时，z 变换就变成了傅立叶变换
• 当 \(\sigma < 0\) 对应 \(s\) 平面的左半平面，对应 \(r < 1\) 即单位圆内部

我们设 \(T_s\) 是抽样周期，\(f_s = 1/T_s\) 为抽样频率，则有

\[\omega=\Omega T_s = 2 \pi f/f_s\]

因此，当 \(f\) 在 \(j\Omega\) 轴上从 \(-\infty\) 到 \(\infty\) 的过程中。每间隔 \(f_s\)，对应 \(\omega\) 从 0 到 \(2\pi\)，即在单位圆上绕了一周。所以从 \(s\) 平面到 \(z\) 平面的映射不是单一的。

由此引出一些重要的定义

• 实际频率 \(f\)，相对连续系统的频率
• 角频率 \(\Omega=2\pi f\)，相对连续系统的角频率
• 归一化频率 \(f'=f/f_s\)
• 圆周频率 \(\omega=2 \pi f'\)

z 变换的收敛域

给出定义，对于 z 变换 \(X(z)\)，使其收敛的 \(z\) 的取值集合称为 z 变换的收敛域 ROC。即有

\[\sum_{n=-\infty}^{\infty}|x(n)r^{-n}|<\infty\]

其中 \(r = |z|\)。因此可以想象收敛域时 \(z\) 平面上一个圆的内部或者外部，即有 \(R_-<|z|<R_+\)。下面有一些例子

例1

令 \(a\) 为常数，\(u(n)\) 为单位阶跃函数。求以下式子 z 变换的收敛域

\[x(n)=a^nu(n)\]

根据定义我们有

\[\begin{split} X(z)&=\sum_{n=-\infty}^{\infty}a^nu(n)z^{-n}=\sum_{n=0}^{\infty} (az^{-1})^n \\\ &=\frac z{z-a} \end{split}\]

显然当 \(|az^{-1}|<1\)，即 \(|z| > |a|\)时，\(X(z)\) 收敛。因此收敛域为 \(a<|z|<\infty\)，图像上为圆半径 \(r=|a|\) 之外的部分

例2

定义同上

\[x(n)=-a^nu(-n-1)\]

其中

\[u(-n-1)=\begin{cases} &1 \ \ \ n \leq -1 \\\ &0 \ \ \ n \geq 0 \end{cases}\]

根据定义我们有

\[\begin{split} X(z)&=\sum_{n=-\infty}^{\infty}a^nu(-n-1)z^{-n}=-\sum_{n=-\infty}^0 (az^{-1})^n \\\ &=\frac z{z-a} \end{split}\]

此时显然有 \(|z|<|a|\) 时收敛。因此收敛域为 \(|z|<a\)，图像上为圆半径 \(r=|a|\) 之内的部分。注意到例 1 和例 2 的 z 变换结果是一样的，但 ROC 不同。因此为了保证由逆 z 变换求出的序列是唯一的，则必须指明 ROC。

例3

定义同上

\[x(n)=a^{|n|}=a^nu(n)+a^{-n}u(-n-1)\]

对于级数 \(a^nu(n)\)，其 z 变换为 \(\frac 1{1-az^{-1}}\)，ROC 是 \(|z|>a\)。对于级数 \(a^{-n}u(-n-1)\)，其 z 变换为 \(\frac 1{1-az}-1\)，ROC 为 \(|z|<\frac 1a\)。因此

\[X(z)=\frac 1{1-az^{-1}}+\frac 1{1-az}-1\]

其 ROC 为 \(a<|z|<\frac 1a\)

显然 \(a>1\) 时不收敛，当 \(a<1\) 时 \(X(z)\) 才收敛。在图像上是一个内径为 \(r=a\) 外径为 \(r=\frac 1a\) 的环

序列与 ROC 的关系

我们设序列 \(x(n)\) 仅在 \(n\) 取值 在 \(N_1\) 与 \(N_2\) 间有值，且\(N_1 < N_2\)。我们可以推演得到以下 ROC 性质。这里特别注意一下，对于有限长的因果序列，其收敛域为 $ |z|>0 $

有限长序列

\(N_1,N_2\)	ROC
\(0 \leq N_1 < N_2 < \infty\)	$ z >0 $
$ -< N_1 < N_2 $	$ z < $
$ -< N_1 < N_2 < $	$ 0 < z < $

右边序列

\(N_1,N_2\)	ROC
\(N_1<0,N_2=\infty\)	$R_{x1}< z < $
\(N_1 \geq 0,N_2=\infty\)	\(\lvert z \rvert >R_{x1}\)

左边序列

\(N_1,N_2\)	ROC
\(N_1=-\infty,N_2>0\)	\(0< \lvert z \rvert <R_{x2}\)
\(N_1=-\infty,N_2 \leq 0\)	\(\lvert z \rvert <R_{x2}\)

双边序列

\(N_1,N_2\)	ROC
\(N_1=-\infty,N_2=\infty\)	\(R_{x1}< \lvert z \rvert < R_{x2}\)

z 变换的性质

线性

若

\[\begin{split} Z[x_1(n)]=&X_1(z),ROC:R_1 \\\ Z[x_2(n)]=&X_2(z),ROC:R_2 \end{split}\]

则有

\[Z[ax_1(n)+bx_2(n)]=aX_1(z)+bX_2(z), ROC:R_1 \bigcap R_2\]

时移性质

对于双边 z 变换有

\[\begin{split} Z[x(n-k)]&=\sum_{n=-\infty}^{\infty}x(n-k)z^{-n} \\\ &=\sum_{m=-\infty}^{\infty}x(m)z^{-m}z^{-k}=z^{-k}X(z) \end{split}\]

但对于单边 z 变换则稍微有点不同。如果 \(x(n)\) 是因果序列

\[Z[x(n-k)] = z^{-k}X^+(z)=z^{-k}X(z)\] \[\begin{split} Z[x(n+k)] =& z^k[X^+(z)-\sum_{n=0}^{k-1}x(n)z^{-n}] \\\ =& z^k[X(z)-\sum_{n=0}^{k-1}x(n)z^{-n}] \end{split}\]

加权性质

若

\[Z[x(n)]=X(z),ROC:R_1 < \lvert z \rvert < R_2\]

则

\[Z[a^nx(n)]=Z(z/a),ROC: \lvert a \rvert R_1 < |z| < |a| R_2 \]

\[Z[nx(n)]=-z \frac d{dz} X(z),ROC:R_1 < |z| < R_2\]

时域卷积性质

记 \(x(n),y(n)\) 的 z 变换分别时 \(X(z),Y(z)\)，则

\[Z[x(n)*y(n)]=X(z)Y(z)\]