FBank与MFCC 计算
MFCC 是语音识别里比较重要的概念,用于声学建模。基本步骤如下
- 将音频按照 10ms步进,20-30ms 长度切片
- 计算每一帧的功率谱周期图(periodogram estimate of the power spectrum)
- 计算 mel filterbank
- 计算 filterbank energy, 对 filterbank energy 求对数
- 计算 log filterbank energy 的 DCT 系数,取前 12 或者 26 个系数
步骤详解
1. 音频切分
我们假设一帧 16KHz 音频有 400 个采样点(即 25ms 时长),其原始信号为 \(s(n)\)。同时我们记 \(s_i(n)\) 为第 \(i\) 帧第 \(n\) 个采样点。
2. 计算 periodogram estimate of the power spectrum
我们首先计算信号的 DFT 如下
\[S_i(k)=\sum^N_{n=1}s_i(n)h(n)e^{-j2\pi kn/N}\ \ 1 \le k \le K\]
\(K\) 为 DFT 长度,\(h(n)\) 为长度为 \(N\) 的信号窗(比如汉明窗)。periodogram estimate of the power spectrum 便可以通过下式计算得到
\[P_i(k)=\frac1N|S_i(k)|^2\]
方便起见我们取 \(K=512\) 且只取 \(S_i(k)\) 的前 257 个系数,这些系数其实代表了各个频率上的能量。
3. 计算 mel filterbank
梅尔刻度利用了人耳对低频声音的频率变化较为敏感的特效,公式如下:
\[M(f)=2595 \log_{10}(1+\frac{f}{700})\]
逆运算为
\[M^{-1}(m)=700(e^{\frac{m}{1127}}-1)\]
一般我们取 300Hz 到 8000Hz 的音频,假如我们要 10 个梅尔三角窗,那么先计算300Hz 和 8000Hz 对应的梅尔刻度为 401.25 Mels/2834.99 Mels 。然后我们再均分得到12个梅尔刻度:401.25, 622.50, 843.75, 1065.00, 1286.25, 1507.50, 1728.74, 1949.99, 2171.24, 2392.49, 2613.74, 2834.99。将这些梅尔刻度再转换为频率便得到 300, 517.33, 781.90, 1103.97, 1496.04, 1973.32, 2554.33, 3261.62, 4122.63, 5170.76, 6446.70, 8000 这 12 个频率点,方便起见我们记为\(f_m(i)\)。
然后我们需要在能量谱里面找到对应的数据点(就是那257个系数),可以用下面的公式
\[ f(i) = floor((K+1)*f_m(i)/samplerate) \]
算得 \(f(i)\) 结果为 9, 16, 25, 35, 47, 63, 81, 104, 132, 165, 206, 256。这里第 256 个点刚好对应了 8 KHz 处。根据这 12 个点可以得到 10 个三角窗如图
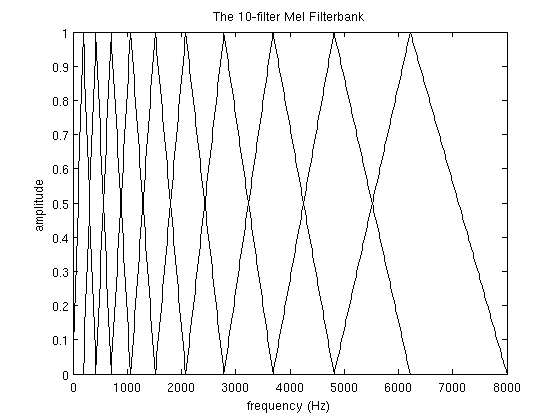
4. 计算 filterbank energy 的对数
我们取 20-40 个梅尔三角窗(标准是26个),对上一步得到的 257 个系数进行加窗(其实就是点乘),就可以得到 26 个 257 维的能量谱,将这 26 个能量谱内的 257 个系数分别加起来,然后对其求对数,便得到了 filterbank energy(26维)。为什么要求对数?因为人耳对声音响度不是线性的。
实际上,这个就是我们所说的 FBank。
5. 计算 filterbank energies 的 DCT 系数
对 fbank 计算 DCT。离散余弦变换(DCT)我个人觉得和 DFT 差不多,只是它的结果都是实数而已。公式似乎还有很多种变形,这里就不贴了,详见 wiki。
我们取 DCT 的前 2-13 个系数,就是 MFCC 了。
思考
MFCC 的好处在于可以减轻混叠,但是它其实损失了 FBank 的一些信息。如果后面是接的深度学习的模型,其实 FBank 就够了