DTW 算法简介
DTW 算法用于解决语音序列不对齐的问题。因为不同的人发言速度不一样,所以很难直接比对两个序列的相似性。
比如下图,将两个序列中相关联的点用虚线连接的话,就会发现这两个序列实际上是很相似的,但如果直接用严格对齐的方式,就显然不对了。
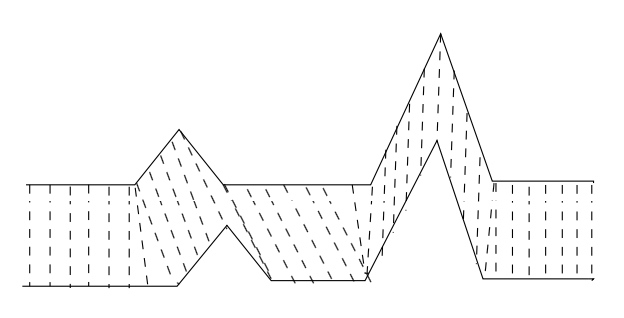
定义
假设我们现在有一个标准的参考模板 \(X\),是一个 \(M\) 维的向量 \(R=\{x_1,x_2,...,x_m\}\)。这里 \(x_1,x_2,...,x_m\) 可以是个特征向量。然后我们有一个需要测试其相似度的模版 \(Y=\{y_1,...,y_n\}\)。注意这里 \(n\) 和 \(m\) 不一定要相等。
问题转化
我们可以将 \(X\) 和 \(Y\) 投射到二维矩阵上。每个小方块代表了 \(x_i\) 到 \(y_j\) 的映射。如下图
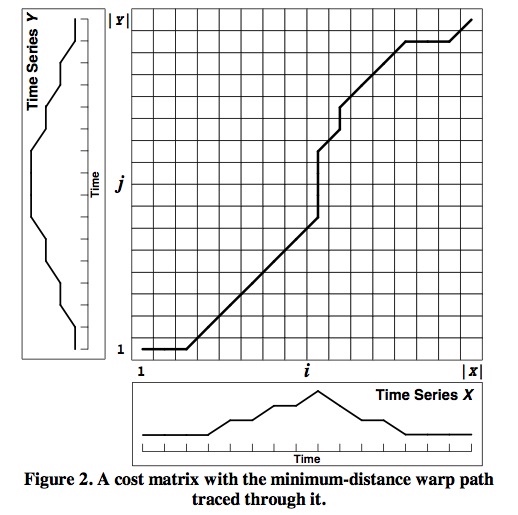
两个序列中点与点之间的关联关系,就可以用这个二维矩阵 \(W\) 来表述。比如,可以用 \(W(i,j)\) 表示第1个序列中的第 \(i\) 个点和第2个序列中的第 \(j\) 个点相对应。所有这样的 \(W(i,j)\) 最终构成了上图中的曲线。这条曲线也被称作归整路径。
当然还是有一定的约束条件的
- 边界条件:\(w_1=(1,1)\) 和 \(w_k=(m, n)\)。首尾需要对齐
- 连续性和单调性:如果 \(w_{k-1}=(a',b')\),那么对于路径的下一个点 \(w_{k}=(a,b)\) 需要满足 \(0 \le a-a' \le 1\) 和 \(0 \le b-b' \le 1\)
因此,如果当前位置为 \(w_{k}=(a,b)\),那么下一个点只有3种可能性 \((a+1,b)\),\((a,b+1)\),\((a+1,b+1)\)
所以最终递推公式如下
\[\begin{aligned} D(i,j)&=Dist(i,j)+\min(D(i-1,j),D(i,j-1),D(i-1,j-1)) \\ D(1,1)&=0 \end{aligned}\]