ASR解码器详解

解码本质上是使用声学模型 \(p(O,S|W)\) 和语言模型 \(P(W)\) 在搜索空间里寻找最可能的词序列 \(\hat{W}\)。

假设句子 \(W\) 由 \(M_W\) 个词组成，\(W=w_1...w_{M_W}\)。那么

\[\begin{aligned} \hat{W} &= \underset{W \in W_{all}}{\arg max} \Big\{ \sum_{S \in S_W}p(O,S|W)P(W) \Big\} \\ &=\underset{W \in W_{all}}{\arg max} \Big\{ \sum_{S \in S_W} \prod_{m=1}^{M_W}p(o^{t_m}_{t_{m-1}+1},s^{t_m}_{t_{m-1}+1}|w_m)P(w_m|w_1^{m-1}) \Big\} \\ &=\underset{W \in W_{all}}{\arg max} \Big\{ \sum_{T \in T_W} \prod_{m=1}^{M_W}\hat{p}(o^{t_m}_{t_{m-1}+1}|w_m)P(w_m|w_1^{m-1}) \Big\} \end{aligned}\]

\(W_{all}\) 为所有的合法词序列

\(S_W\) 表示词序列 \(W\) 可以对应的所有合法状态序列。

\(p(o_a^b,s_a^b|w)\) 表示词 \(w\) 沿着状态序列 \(s_a,...,s_b\) 生成语音片段 \(o_a,...,o_b\) 的概率。

\(t_{m-1}+1\) 为词 \(w_m\) 对应的观察的第一帧下标， \(t_m\) 为词 \(w_m\) 对应的观察的最后一帧下标，即 \(t_{m-1}+1,...,t_m\) 是 \(w_m\) 对应 \(w_m\) 观察序列。

\(T_W\) 代表词序列 \(W\) 所有可能的结束帧的序列（间接表示了一种对齐方式），即 \(T \in T_W\) 是一个时间序列 \(t_1,...,t_{M_W}\)，表示了词序列 \(w_1,...,w_{M_W}\) 每个词最后一帧的时间。

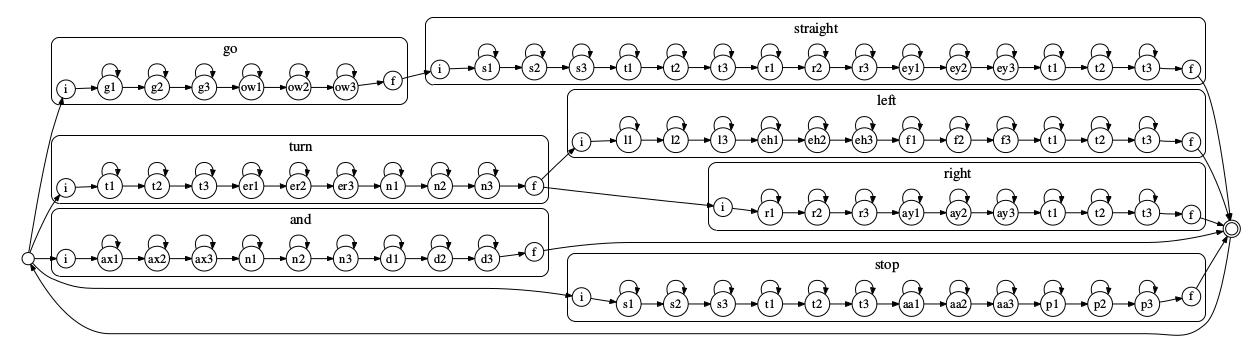
在这里我们将整个模型转换为可以用 Viterbi 算法求解的 HMM 最佳状态序列的问题。这个 HMM 大约有 \(|\overline{S}| |Q|\) 个状态。\(|\overline{S}|\) 为每个词 HMM 平均状态数，|Q| 为 FSQ 状态数（有限状态文法，表示语言模型）。可以认为 FSG 里每个状态就是一个词，状态之间的边表示可以从一个词跳转到另外一个词，把每个状态展开成这个词对应的 HMM，就得到了大的 HMM。一个例子如下