PRML笔记 - 贝叶斯与 Beta 分布
这篇是关于贝叶斯的第二部分。主要讲讲 Beta 分布。
伯努利分布
我们考虑一个简单的伯努利分布,即抛一枚不均匀的硬币,\(x=1\) 表示正面,\(x=0\) 表示反面,\(x=1\) 的概率被记为 \(\mu\)。
\[Bern(x|\mu ) = {\mu}^x{(1-\mu )}^{1-x}\]
假设我们已经有针对随机变量 \(x\) 的一系列观测 \(D={x_1, x_2, ..., x_n}\),那么可以得到关于 \(\mu\) 的似然函数如下
\[p(D|\mu)=\prod_{n=1}^N \mu^{x_n}(1-\mu)^{1-x_n}\]
\[\ln p(D|\mu)=\sum^N_{n=1}\{x_n \ln \mu+(1-x_n) \ln(1-\mu)\}\]
应用极大似然法,令 \(\ln p(D|\mu)\) 关于 \(\mu\) 的导数为0,估计其参数 \(\mu\) 的结果为
\[{\mu}_{ML} = \frac{1}{N}\sum^{N}_{n=1}x_n\]
实际上极大似然法是有缺陷的。假设我们抛了 3 次硬币,每次都是正面。那么根据极大似然法得到的对于 \(\mu\) 的估计就是 1。这显然就是瞎扯淡,我们需要加入一个先验来修正这一点。
Beta 分布
我们对 \(\mu\) 给定一个 Beta 分布的先验信息如下
\[Beta(\mu|a,b)=\frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)}{\mu}^{a-1}(1-\mu)^{b-1}\]
\[\Gamma(x)= \int^{\infty}_0{\mu}^{x-1}e^{-u}du\]
前面的 \(\frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)}\) 用于确保 Beta 分布被正确的归一化,即保证了 \(\int^{\infty}_{-\infty} Beta(\mu|a,b)d \mu=\int^1_0 Beta(\mu|a,b)d \mu=1\)。我其实还蛮好奇这个莫名其妙的系数是怎么来的,虽然 PRML 上没提到,我稍微做了点探索。我们把式子中的 \(\Gamma(a) \Gamma(b)\) 写出来瞅瞅。
\[\Gamma(a) \Gamma(b)=\int^{\infty}_0e^{-x}x^{a-1}dx\int^{\infty}_0e^{-y}y^{b-1}dy\]
我们令 \(t=x+y\),则有
\[\begin{split}\Gamma(b) =& \int^{\infty}_0e^{-y}y^{b-1}dy \\\ =&\int^{\infty}_x e^{x-t}(t-x)^{b-1}dt \end{split}\]
带入回到原来的式子
\[\begin{split}&\int^{\infty}_0e^{-x}x^{a-1}dx\int^{\infty}_0e^{-y}y^{b-1}dy\\\ =&\int^{\infty}_0e^{-x}x^{a-1}dx\int^{\infty}_x e^{x-t}(t-x)^{b-1}dt \\\ =&\int^{\infty}_0 x^{a-1} \left\{ \int^{\infty}_{x}e^{-t}(t-x)^{b-1}dt \right\}dx \\\ =&\int^{\infty}_0 \int^{\infty}_x e^{-t} x^{a-1}(t-x)^{b-1}dt dx \end{split}\]
这里需要交换 \(dx\) 与 \(dt\) 的积分顺序,我们画个图帮助理解一下。积分的范围是图中的阴影部分,即原本的式子是先在 \(t\) 方向上积分,从 \(x\) 积分到 \(\infty\),再在 \(x\) 方向上积分,从 0 积分到 \(\infty\)。交换一下积分顺序,先在 \(x\) 方向上积分,从 0 积分到 \(t\),再在 \(t\) 方向上积分,从 0 积分到 \(\infty\)
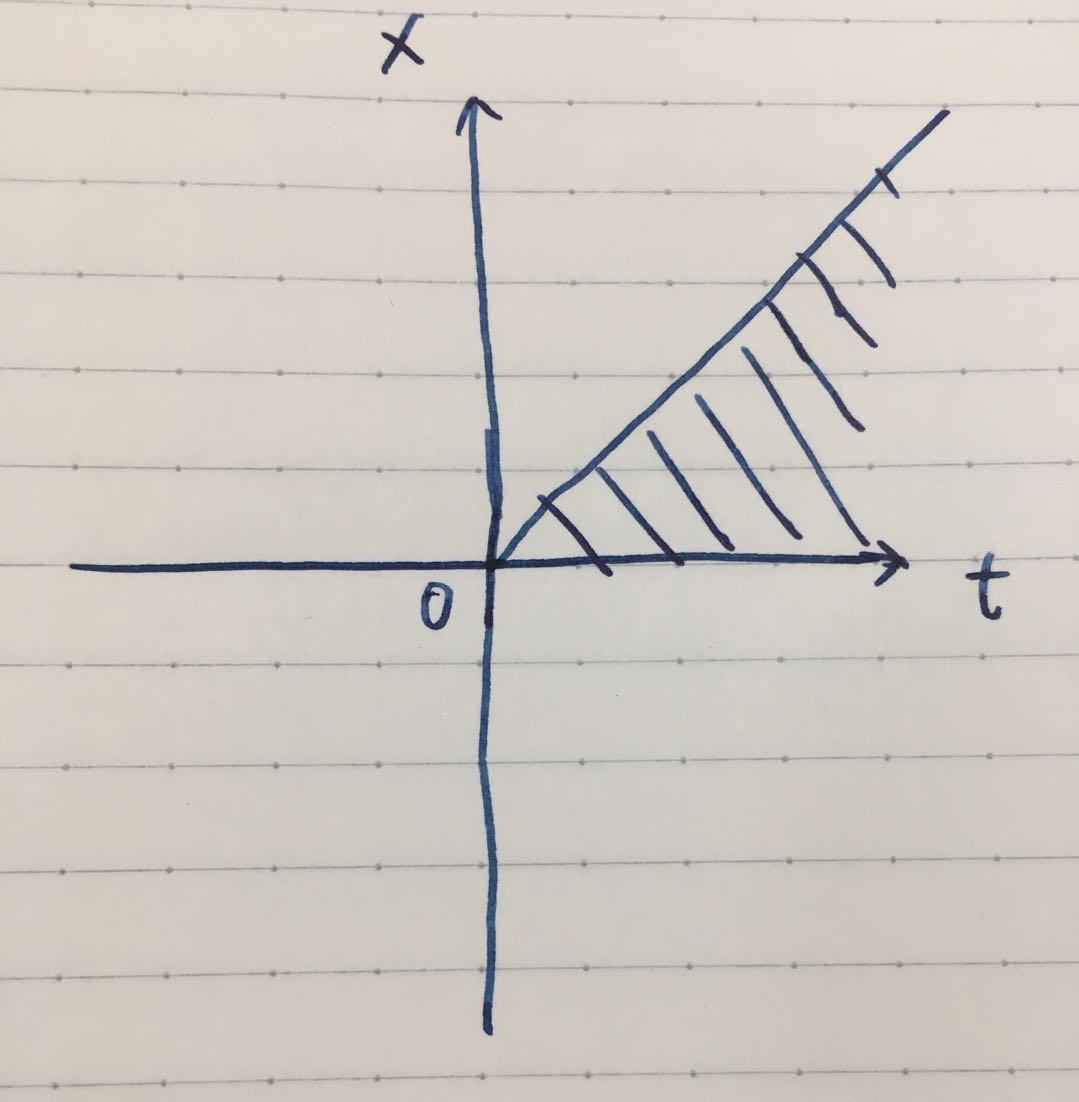
那么我们接着推公式,且记 \(x=t \mu\)
\[\begin{split} &\int^{\infty}_0 \int^{\infty}_x e^{-t} x^{a-1}(t-x)^{b-1}dt dx \\ =& \int^{\infty}_0 \int^t_0 e^{-t} x^{a-1}(t-x)^{b-1} dx dt \\ =& \int^{\infty}_0 \int^1_0 e^{-t} (t \mu)^{a-1}(t-t \mu )^{b-1} d \mu dt \\ =& \int^{\infty}_0e^{-t}t^{a+b-1}dt \int^1_0 \mu^{a-1}(1-\mu)^{b-1}d\mu \\ =& \Gamma(a+b)\int^1_0 \mu^{a-1}(1-\mu)^{b-1}d\mu \end{split}\]
总结一下,就是
\[ \Gamma(a) \Gamma(b) = \Gamma(a+b)\int^1_0 \mu^{a-1}(1-\mu)^{b-1}d\mu \]
回到最开始的式子,容易有
\[\begin{split} \int^1_0Beta(\mu|a,b)d\mu =& \int_0^1 \frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)}{\mu}^{a-1}(1-\mu)^{b-1}d \mu \\ =&\frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)} \int^1_0 {\mu}^{a-1}(1-\mu)^{b-1}d \mu \\ =& 1 \end{split}\]
Beta 分布的均值和方差为
\[E[\mu] = \frac{a}{a+b} \\ var[\mu]=\frac{ab}{(a+b)^2(a+b+1)}\]
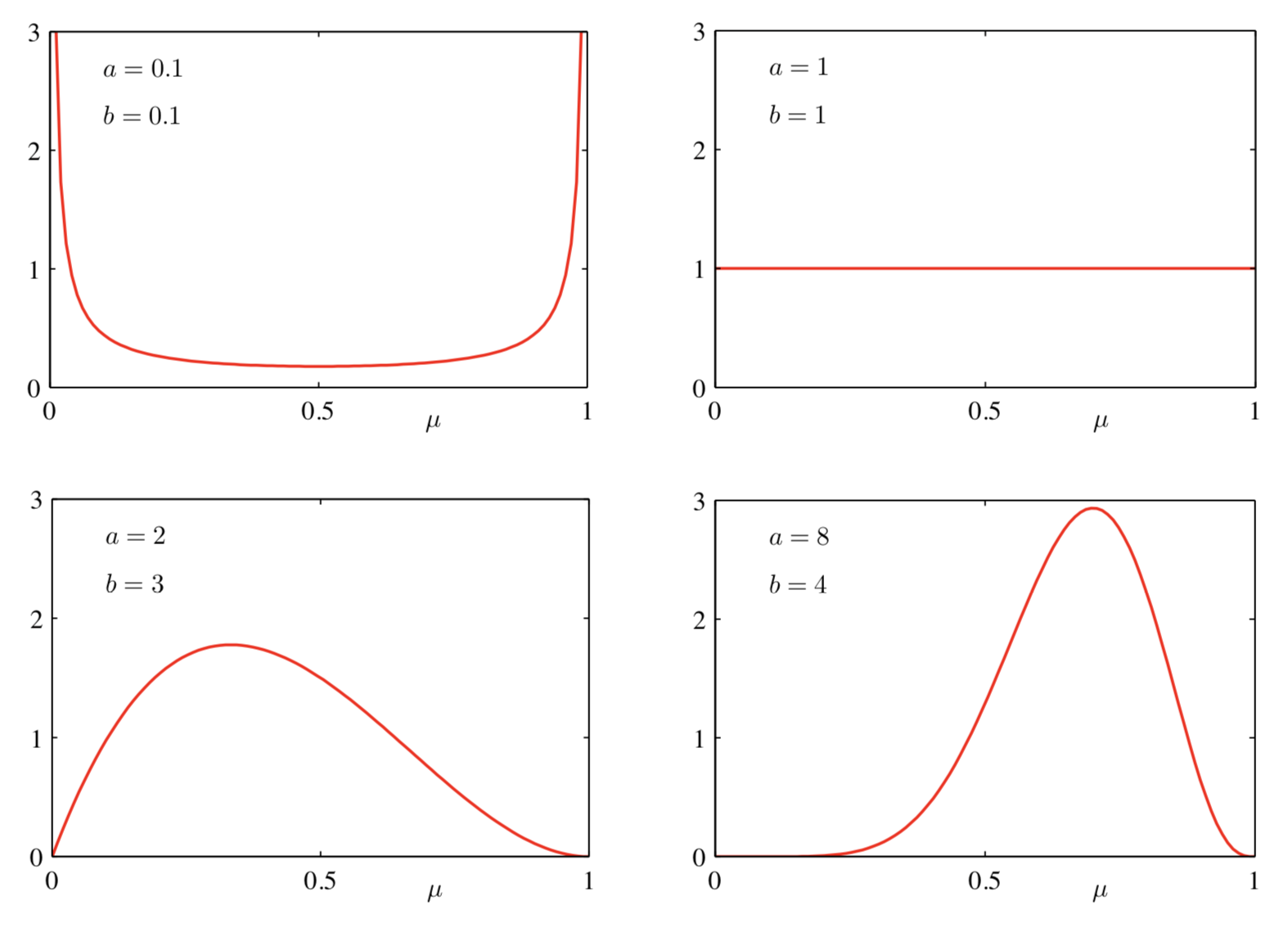
参数 \(a,b\) 控制了参数 \(\mu\) 的(先验)概率分布,所以也称之为超参数。直接拿了几张 PRML 里的图展示一下不同 \(a,b\) 对应的 Beta 分布图像
Beta 分布与顺序方法
在刚开始看 Beta 分布的时候我很好奇,为什么要用这样一个分布去当先验,用高斯不好么。后来才发现用 Beta 分布可以应用顺序方法,因为 Beta 分布是伯努利似然函数的共轭先验(通俗点说就是 Beta 分布乘以似然函数还是一个 Beta 分布)。
设我们现在抛了 \(N\) 次硬币,有 \(m\) 次正面朝上,\(l\) 次反面朝上。我们把 Beta 先验乘以二项似然函数,去掉前面与 \(\mu\) 无关的系数,有
\[\begin{split} &\frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)}{\mu}^{a-1}(1-\mu)^{b-1} {\mu}^m{(1-\mu )}^l \\=&\frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)}{\mu}^{m+a-1}(1-\mu)^{l+b-1} \\ \propto&{\mu}^{m+a-1}(1-\mu)^{l+b-1} \end{split}\]
实际上,这个后验概率还是 Beta 分布的形式,我们根据之前的推导可以得到它的归一化系数。
\[p(\mu | m,l,a,b)=\frac{\Gamma(m+a+l+b)}{\Gamma(m+a)\Gamma(l+b)}{\mu}^{m+a-1}(1-\mu)^{l+b-1}\]
可以这么理解,在原来的先验基础上,观察到 \(m\) 次正面朝上,意味着 Beta 分布的 \(a\) 增加了 \(m\),观察到 \(l\) 次反面朝上,Beta 分布的 \(b\) 增加了 \(l\)。直接抄一个 PRML 上面的例子。先验的 Beta 分布参数 \(a=b=2\),观察到一次正面朝上,后验概率就是 \(Beta(\mu|a=3,b=2)\)
一个自然的想法就是顺序方法。我们不再一次性读入所有的观测数据,而是一次读入一个,逐渐更新概率分布。
推广到多项式变量
对于有 \(K\) 个状态的随机变量,它其实是二元变量的自然推广。我们约定如下的变量表示方法:对于 \(K=6\),如果取到了第 3 个状态,则状态量 \(\boldsymbol{x}\) 表达如下
\[\boldsymbol{x}=(0,0,1,0,0,0)^T\]
需要满足 \(\sum_{k=1}^Kx_k=1\)。参数 \(\mu_k\) 表示 \(x_k=1\) 的概率,那么我们可以用列向量 \(\boldsymbol{\mu}\) 来表达取到各个状态的概率,\(\boldsymbol{\mu}=(\mu_1,...,\mu_K)^T\)。需要满足 \(\mu_k \geq 0\) 和 \(\sum_{k=1}^Kx_k=1\)。我们略去推到过程,直接给出结论。
假设我们有 \(m_1+m_2+...+m_K=N\) 次观测,\(m_k\) 为状态 \(k\) 的观测次数。多项式分布的形式为
\[Mult(m_1, m_2,...,m_K|\boldsymbol{\mu},N)=\frac{N!}{m_1!m_2!...m_K!}\prod_{k=1}^{K}{\mu_k}^{m_k}\]
对于有 \(N\) 个独立观测 \(\boldsymbol{x}_1,...,\boldsymbol{x}_N\) 的数据集 \(D\),设 \(m_k\) 为观测到 \(x_k=1\) 的次数。则它的似然函数为
\[p(D|\mu)=\prod_{k=1}^K{\mu}^{m_k}\]
对应的共轭先验为狄利克雷分布
\[ Dir(\boldsymbol{\mu}|\boldsymbol{\alpha})=\frac{\Gamma(\sum_{k=1}^K {\alpha}_k)}{\Gamma({\alpha}_1)...\Gamma({\alpha}_K)}\prod^K_{k=1} {\mu}_k^{\alpha_k-1}\]
同样可以应用顺序方法,每观测到一个新的值,就可以去更新参数 \(\boldsymbol{\alpha}\)。