N-gram 与 Viterbi 算法
这一回我们讲讲如何在 N-gram 模型中使用维特比算法进行连续语音识别。
N-gram 模型
N-gram 本质上是一个统计模型,它的思想很简单。假设一个长度为 \(M\) 的词序列为 \(w_1^M=\{w_1,...,w_M\}\),那么我们有
\[P(W)=\prod_{m=1}^M P(w_m|w_1^{m-1})\]
N-gram 就是把概率 \(P(w_m|w_1^{m-1})\) 近似为 \(P(w_m|w_{m-n+1}^{m-1})\)。就是说,下一个词的概率只和前 \(N\) 个词有关。N-gram 模型也可以看做是 \(N-1\) 阶的马尔科夫模型(注意这里是马尔可夫模型,而不是 HMM),它的每个状态只依赖于之前的 \(N-1\) 个时刻,而与更久之前的历史无关。
对于 N-gram 模型,它可以表达为 WFSA,需要有 \(|V|^{n-1}\) 个状态以及 \(|V|^n\) 个跳转,这里 \(|V|\) 为词典的大小,每个状态表示 \(N-1\) 个词的历史,而每一个跳转表示出现下一个词的概率。
搜索空间
假设句子 \(W\) 由 \(M_W\) 个词组成,\(W=w_1...w_{M_W}\)。那么我们需要搜索最佳路径如下
\[\begin{aligned} \hat{W}=&\arg \max_{W \in \omega}\{\sum_{S \in S_W}p(O,S|W)P(W)\} \\ =&\arg \max_{W \in \omega} \{\sum_{S \in S_W} \prod_{m=1}^{M_W} p(o_{t_{m-1}+1}^{t_m},s_{t_{m-1}+1}^{t_m}|w_m)P(w_m|w_1^{m-1}) \} \end{aligned}\]
解释一下,\(p(o_a^b,s_a^b|w)\) 表示词 \(w\) 沿着状态序列 \(s_a,...,s_b\) 生成语音片段 \(o_a,...,o_b\) 的概率。\(S_W\) 为词序列 \(W\) 可以对应的所有合法状态序列。\(t_m\) 表示词 \(w_m\) 对应的观察的最后一帧的下标,所以 \(t_{m-1}+1,...,t_m\) 是 \(w_m\) 对应的全部观察序列(\(t_m\) 是 \(w_m\) 对应的 HMM 终止状态)
使用 Viterbi 概率来近似,可以把求和变成 max 。求和变求最大,我的理解是:一个词序列可以对应多种状态序列,实际上我们只需要取这个词序列最可能对音的状态序列就可以。因此公式改写如下
\[\begin{aligned} \hat{W}=& \arg \max_{W \in \omega}\{\sum_{S \in S_W}p(O,S|W)P(W)\} \\ =&\arg \max_{W \in \omega } \{\max_{S \in S_W}\prod_{m=1}^{M_W} p(o_{t_{m-1}+1}^{t_m},s_{t_{m-1}+1}^{t_m}|w_m)P(w_m|w_1^{m-1})\} \\ =&\arg \max\{\max_{T \in \tau_W} \prod_{m=1}^{M_W} \tilde{p}(o_{t_{m-1}+1}^{t_m})P(w_m|w_1^{m-1}) \} \end{aligned}\]
这个式子中 \(\tau_W\) 代表词序列 \(W\) 所有可能的结束帧序列(其实间接表示了一种对齐方式)。换句话说 \(T \in \tau_W\) 是一个时间序列 \(t_1,...,t_{M_W}\),表示了词序列 \(w_1,...,w_{M_W}\) 每一个词的最后一帧的时间。
HMM 模型扩展
Viterbi 算法可以高效的估计一个 HMM 模型在给定观测下的最优状态估计,即在上式中,可以高效计算一个词的最优状态序列。但这里我们需要对所有的词序列进行遍历(给定词序列,寻找最佳的时间序列对应方式,再求最大值)。这里我们对 Viterbi 算法进行扩展,即在词之间的增加状态跳转,同时这个跳转会讲语言模型的得分编码进去。
这样一个扩展后的 HMM 大约会有 \(|\overline{S}|*|V|^{n-1}\) 个状态。\(|\overline{S}|\) 是每个词的平均状态数,而 \(|V|^{n-1}\) 是 N-gram 模型的状态数。同时为了方便,我们还会有一个特殊的开始状态和结束状态。
下图是一个简单的例子。每个方块代表一个词,词内的声学模型是 3 状态的 HMM(也可以是其他 HMM),每个状态都可以跳转到自身或者下一个状态。方块之间的跳转代表 N-gram 表示的语言模型。注意到这里还有一个特殊的跳转,直接从结束状态跳回至初始状态,方便进行连续的语音识别。
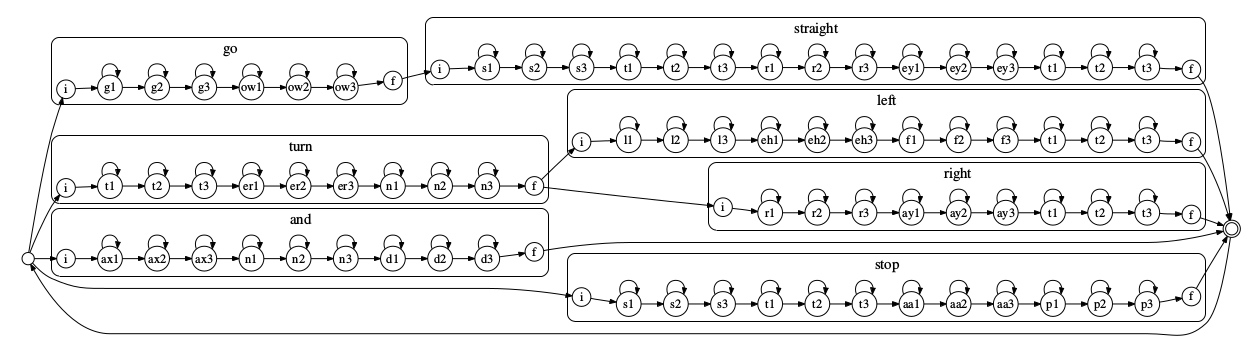
对上面的 HMM 应用维特比算法(输入的观测为声学概率,寻找最佳状态序列),便可以执行连续识别任务。